In the previous lesson we examined the factors that affect the resistance of materials. For a length of wire two of those factors are length, l, and cross-sectional area, A.
We discussed that resistance R is proportional to length, l, and inversely proportional to cross-sectional area, A
That is ,
![]()
Thus we may write,
![]()
where ρ is constant for a given material
ρ is called the resistivity of the material. Its SI unit is Ω.m (Ohm-meter)
Resistivity is independent of the shape of the material, a wire was used as an example to simplify the calculations. (Only two variables, length and CSA).
Resistivity may also be defined in terms of the current density, J, at a particular point in a substance and the electric field, E, at that point.
ρ = E/J
The conductivity, σ, of a material is simply the inverse of its resistivity.
Thus, σ = 1/ρ
Obviously its SI unit is (Ω.m)-1 (mhos per meter).
The resistivity and hence resistance of a substance is affected by its temperature. The reasons were discussed in the previous lesson - Resistance.
Substances for which the resistance increases with temperature is said to have a positive temperature coefficient of resistance.
If the resistance decreases with temperature increase, then the substance has a negative temperature coefficient of resistance.
Finally if the resistance does not vary with temperature then the substance has a zero temperature coefficient of resistance.
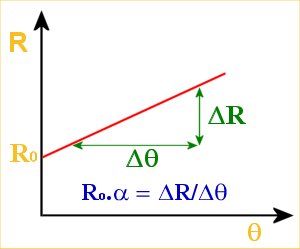
The relationship between temperature and resistance is fairly linear over a wide temperature range. Thus a straight line equation is used in the definition of the temperature coefficient of resistance.
The temperature coefficient of resistance, α :
Rθ = R0 ( 1 + αθ)
where Rθ is the resistance a
particular temperature, θ
and R0 is the resistance at 0°C.
From the equation one can deduce that α has units K-1.
Graph of Resistance vs. Temperature:
We may instead wish to examine the variation of resistivity with temperature. A linear approximation is used giving:
ρ - ρ0 = ρ0 α ( T - T0 )
Where ρ = resistivity at temperature T,
ρ0 = resistivity at selected reference temperature T0
(Usually room temperature, 293K i.e. 20°C)
α = temperature coefficient of resistivity (same as temperature coeff. of
resistance)
If ( ρ - ρ0 ) is plotted against ( T - T0 ) then the gradient of the resultant plot would be ρ0 α
Iron has a resistivity of 9.68 * 10-8 Ω.m at 293K.
R = ρl/A
1.a Answer:
The block has length 20cm (0.2m) and cross-sectional area 2*2 cm (0.02 * 0.02)m2 = 0.0004m2
Thus R = (9.68 * 10-8 * 0.2)/0.0004 Ω = 48.4 μΩ.
1.b Answer:
Length, l = 2cm = 0.02m
Cross-sectional Area, A = 0.02 * 0.2 = 0.004m2
Thus R = (9.68 * 10-8 * 0.02)/0.004
Ω = 0.484 μΩ.
These answers confirm that is it easier for current to flow through a short, fat conductor than a long and narrow conductor.
Solution for 2
R = ρl/A
Transposing,
l = AR/ρwhere R = 0.33 Ω, ρ = 100 * 10-8 Ωm,
A = πr2, r = 1mm (0.001m)
thus, A = 3.142 * 10-6 m2.hence.
l = (3.142 * 10-6)(0.33)/(100 * 10-8)
l = 10.4mmAnswer: 10.4mm of nichrome wire is needed
Solution for 3
Rθ = R0 ( 1 + αθ)
where R0 = 0.33 Ω, α = 4 * 10-3 K-1, θ = 40°C
Hence
Rθ = (0.33)(1 + [4 * 10-3 * 40])
Rθ = 0.383ΩAnswer: The nichrome wire now has a resistance of 0.383Ω.
| Material | Resistivity (Ωm) | Temp. Coeff.of Resistivity (K-1) |
|
Metals |
||
| Silver | 1.62 * 10-8 | 4.1 * 10-3 |
| Copper | 1.69 * 10-8 | 4.3 * 10-3 |
| Aluminum | 2.75 * 10-8 | 4.4 * 10-3 |
| Tungsten | 5.25 * 10-8 | 4.5 * 10-3 |
| Iron | 9.68 * 10-8 | 6.5 * 10-3 |
| Platinum | 10.6 * 10-8 | 3.9 * 10-3 |
| Manganin | 48.2 * 10-8 | 0.002 * 10-3 |
|
Semiconductors |
||
| Pure Silicon | 2.5 * 103 | -70 * 10-3 |
| n-type Silicon | 8.7 * 10-4 | |
| p-type Silicon | 2.8 * 10-3 | |
|
Insulators |
||
| Glass | 1010 - 1014 | |
| Fused Quartz | ~ 1016 | |
As the table shows metals have positive temperature coefficients of resistivity as well as low resistivities.
Silicon, which is a semiconductor, has a negative temperature coefficient of resistivity an a fairly high resistivity.
Insulators such as glass and fused quartz are characterized by very high resistivities. (Very high resistance → Very low or no current flow even when subjected to high pd's → good insulator)
The table shows that silver is the best conductor, then copper then aluminum. Conductivity however is not the only factor to consider when choosing electrical conductors. Availability and cost must also be considered.
Power Transmission lines are made from aluminum because it is the cheapest of the three and the losses incurred (heat losses due to resistance of lines) are not significant enough to warrant using the rarer and more expensive copper.
Telephone lines are typically copper. The low resistivity and good noise immunity offered are necessary for transmission of low power communication signals.
Silver being the most expensive is only used in small components where copper would not be appropriate. IC packages sometimes use silver leads.