Many readers already have informal knowledge of electricity. Many people are familiar with the terms AC and DC electricity but they do not fully appreciate the meaning of those terms. By the end of this lesson readers will develop an understanding of these concepts.
Specifically, you will be able to:
Some readers may be thinking," How crazy is this guy? He wants to talk about sources of AC and DC electricity before discussing what they are."
Well, you are already familiar with AC and DC electricity - at least familiar enough to make sense of the following list.
AC Sources:
DC Sources:
AC - Alternating Current,
DC - Direct Current,
Way back when we studied Ohm's Law we learned that electricity in a metal wire was a flow of electrons in a particular direction.
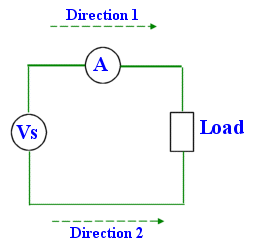
Let us consider the measurement of the flow of current in a circuit.

There are two dimensions to consider, magnitude and direction. Magnitude is a measure of the amount of current - a measure of quantity. At any given instant 3 million electrons may be drifting through a particular cross-section of the wire or maybe only 50 thousand.
The diagram above indicates that there are two directions for electricity to flow around the circuit - clockwise or anti-clockwise. These directions are detectable. Current flowing clockwise will cause the moving coil ammeter to deflect in one direction while anticlockwise current will cause a deflection in the opposite direction. (You will learn more about this when you study Magnetism and Electromagnetism).
Since there are only two direction we are interested in (clockwise or anticlockwise) the direction component may be represented as a sign, plus or minus. Thus the directed number system can be used to represent both magnitude and direction
For example if 10V represents a fixed amount of current flowing clockwise around a circuit then -10V represents the same amount of current flowing anticlockwise around the circuit.
Now that we understand magnitude and direction let us define DC and AC.
Let's represent these definitions graphically.
 |
 |
|
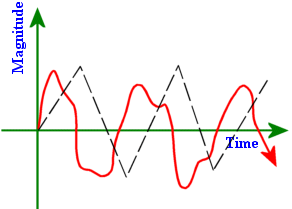
2 Examples of AC waveforms |
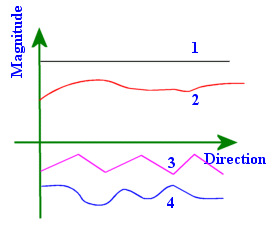
4 Examples of DC waveforms |
Note that in AC waveforms both magnitude and directions change.
With reference to the graph of 4 DC waveforms, currents 1 and 2 are in one direction while 3 and 4 are in the opposite direction.
Pay close attention to waveform 1. Both the magnitude and direction are time-invariant. Such a waveform is what we commonly refer to as DC. This constant magnitude DC waveform is generated by sources such as car batteries and dry cells.
The AC waveform that is generated by the power company is sinusoidal in nature. When we refer to AC we are generally considering the sinusoidal waveform.
 |
| Sinusoidal AC Graph showing Amplitude, RMS, and Average Value |
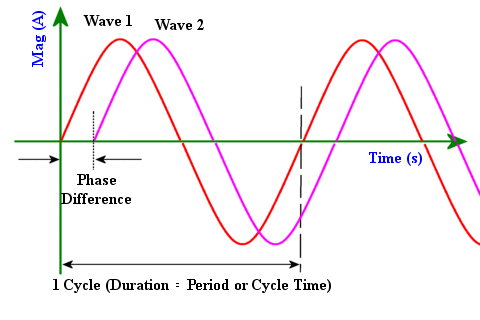 |
| Sinusoidal AC Graph showing phase, cycle and frequency |
As you can see from the above graphs the sinusoid is a symmetrical wave. The area above and below the time axis is the same for a cycle giving an average magnitude of 0.
The trough and peak magnitudes have the same absolute value which is know as Amplitude.
The root mean square value is computed as 1/√2 of the Amplitude. A constant DC of RMS value has the same heating effect in a resistor as the AC sinusoid. When we refer to the magnitude of an AC wave we use the RMS rather than the amplitude. Thus when we say that the AC mains is 120V we actually mean that the RMS is 120V. The amplitude is √2 * 120 = 169.7V
The AC sinusoid is a repeating pattern. The fundamental unit of this pattern is one cycle. The duration of a cycle is known as the cycle time or period. The SI unit of period is the second.
The frequency, f, is computed as the
inverse of the period, T, i.e. f = 1/T.
As you may have guessed the SI unit for frequency is s-1.
This unit is called the Hertz (Hz).
Wave 2 crosses zero after wave 1, i.e. wave 1 leads wave 2 or wave 2 lags wave 1. Both waves are identical except for the time delay separating them. This temporal separation is what is referred to as a phase difference. When comparing phases it is usual to compare angular separation rather than time.
Mathematical Representation of a sinusoid:
![]()
where M = magnitude at time t,
A = amplitude,
T = period,
φ = phase angle in degrees
Answer:
The DC current has magnitude equal to the RMS value of the AC. i.e. 0.707 * 15
= 21.2V
Answer:
1 Period = 360°
But Period, T = 1/60 = 16.7ms
Thus 16.7ms = 360°
→ 1ms = (360/16.7)°
and 4.17ms = (360°/16.7ms) * 4.17ms = 89.9°
The phase difference is 89.9°
Answer:
T = 1/f = 1/20 = 20ms
RMS = 0.707 * 12 = 17A
Answer:
Waveform A : Amplitude = 10V, Frequency = 50Hz, Phase = 0 degrees
Required waveform, B, must have a magnitude that is equal to A's but be in the opposite direction at all times.
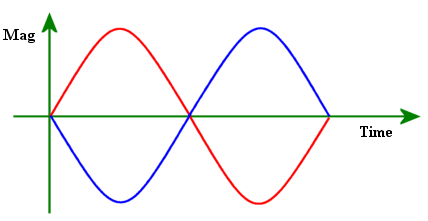
From the above diagram it is clear that B is A with a 180°
phase delay.
